Selected Publications
A list of selected publications of Dr. Errami
Book
Efficient Methods for Symbolic Analysis of Complex Reaction Networks
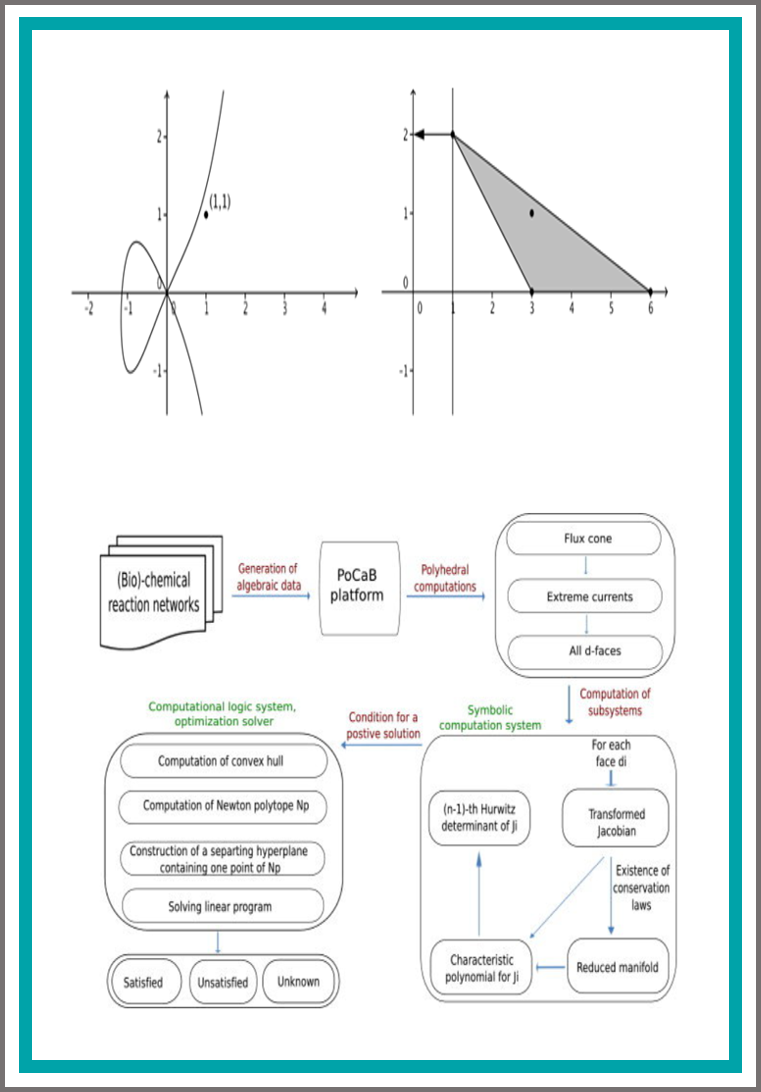
In this Book, I mainly present efficient algorithmic methods to detect Hopf bifurcation fixed points in (bio)-chemical reaction networks with symbolic rate constants, thereby yielding information about their oscillatory behavior of the networks. The methods use the representations of the systems on convex coordinates that arise from stoichiometric network analysis. One of the methods called HoCoQ reduces the problem of determining the existence of Hopf bifurcation fixed points to a first-order formula over the ordered field of the reals that can then be solved using computational-logic packages. The second method called HoCaT uses ideas from tropical geometry to formulate a more efficient method that is incomplete in theory but worked very well for the attempted high-dimensional models involving more than 20 chemical species. We also study Muldowney's extension of the classical Bendixson-Dulac criterion for excluding periodic orbits to higher dimensions for polynomial vector fields and we discuss the use of simple conservation constraints and the use of parametric constraints for describing simple convex polytopes on which periodic orbits can be excluded.

Sensors - Open Access
Unsupervised and Generic Short-Term Anticipation of Human Body Motions
Various neural network based methods are capable of anticipating human body motions from data for a short period of time. What these methods lack are the interpretability and explainability of the network and its results. We propose to use Dynamic Mode Decomposition with delays to represent and anticipate human body motions. Exploring the influence of the number of delays on the reconstruction and prediction of various motion classes, we show that the anticipation errors in our results are comparable or even better for very short anticipation times (<0.4 sec) to a recurrent neural network based method. We perceive our method as a first step towards the interpretability of the results by representing human body motions as linear combinations of ``factors''. In addition, compared to the neural network based methods large training times are not needed. Actually, our methods do not even regress to any other motions than the one to be anticipated and hence is of a generic nature.

Journal of Symbolic Computation
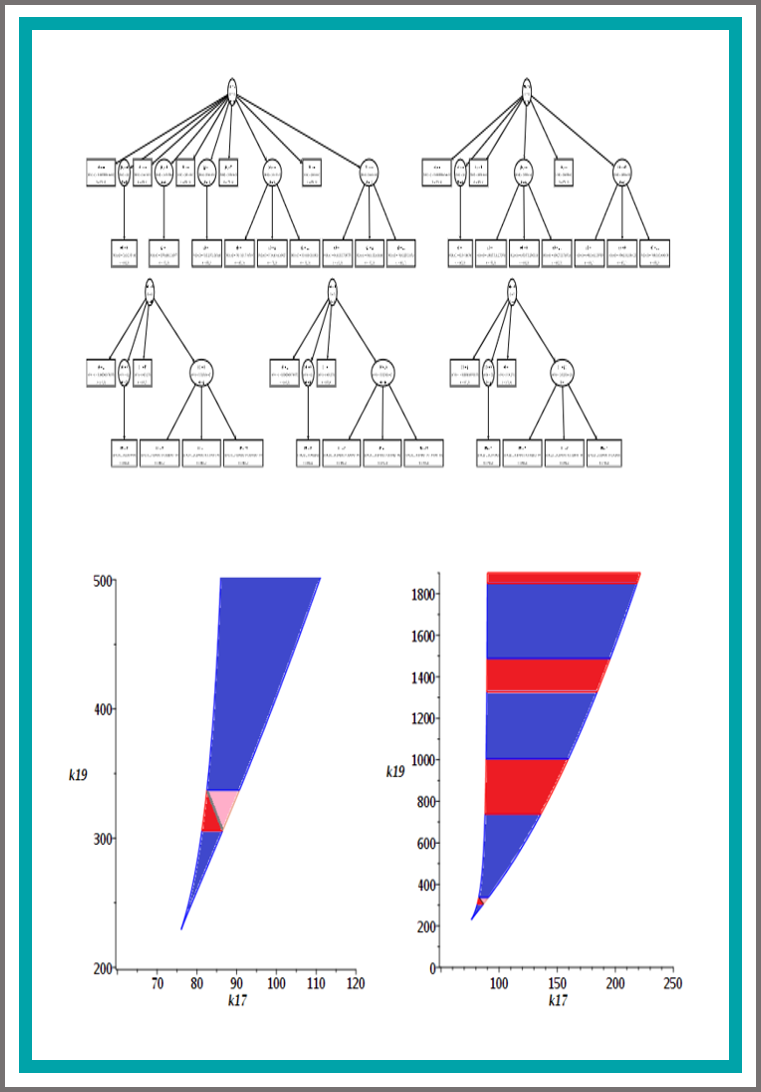
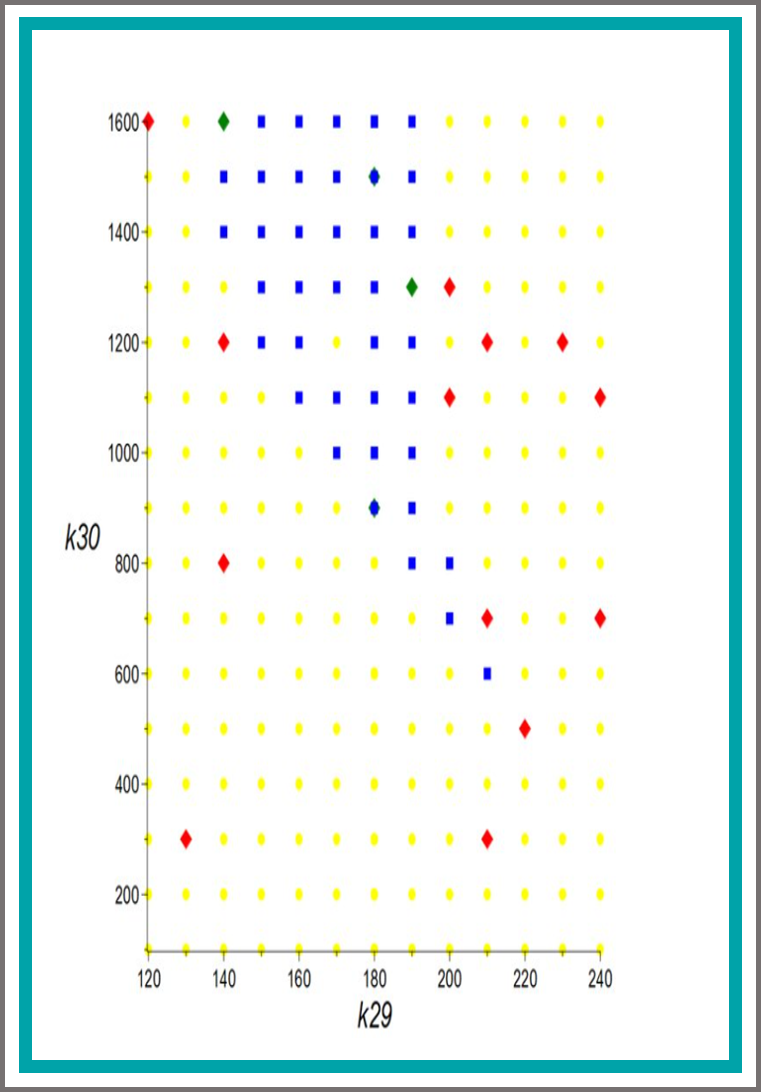
Identifying the parametric occurrence of multiple steady states for some biological networks
We consider a problem from biological network analysis of determining regions in a parameter space over which there are multiple steady states for positive real values of variables and parameters. We describe multiple approaches to address the problem using tools from Symbolic Computation. We describe how progress was made to achieve semi-algebraic descriptions of the multistationarity regions of parameter space, and compare symbolic results to numerical methods. The biological networks studied are models of the mitogen-activated protein kinases (MAPK) network which has already consumed considerable effort using special insights into its structure of corresponding models. Our main example is a model with 11 equations in 11 variables and 19 parameters, 3 of which are of interest for symbolic treatment. The model also imposes positivity conditions on all variables and parameters. We apply combinations of symbolic computation methods designed for mixed equality/inequality systems, specifically virtual substitution, lazy real triangularization and cylindrical algebraic decomposition, as well as a simplification technique adapted from Gaussian elimination and graph theory. We are able to determine multistationarity of our main example over a 2-dimensional parameter space. We also study a second MAPK model and a symbolic grid sampling technique which can locate such regions in 3-dimensional parameter space.
IEEE Acces
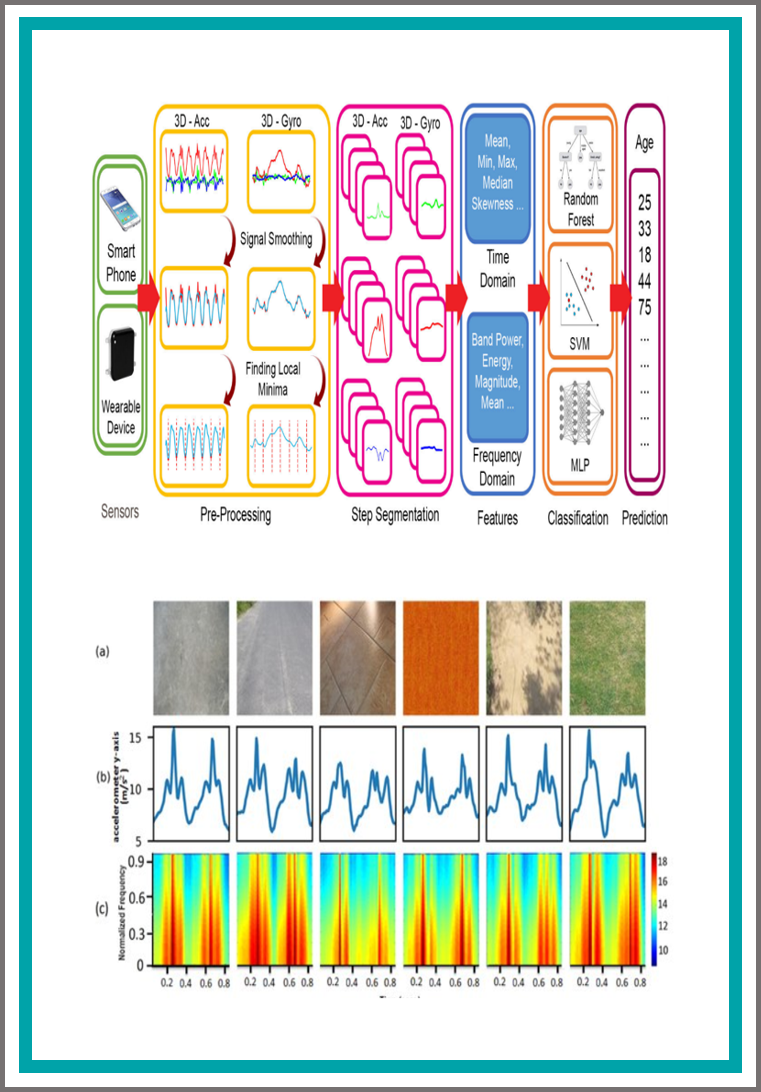
Move Your Body: Age Estimation Based on Chest Movement During Normal Walk
The estimation of soft biometrics of a subject, including age, through the gait analysis is a challenging area of research due to variations in individuals’ gaits and the effect of ageing on gait patterns. In this paper, we present the results of age estimation based on the analysis of inertial data of human walk. We have recorded 6D accelerations and angular velocities of 86 subjects while performing standardized gait tasks using chest-mounted inertial measurement units. The recorded data were segmented to decompose the long sequences of signals into single steps. For each step, we compute a total of 50 spatio-spectral features from 6D components. We trained three different machine learning classifiers—random forests, support vector machines, and multi-layer perceptron—to estimate the human age. Two different types of cross validation strategies, i.e., tenfold and subjectwise cross validation were employed to gauge the performance of the estimators. The results reveal that it is possible to predict the age of a subject with higher accuracy.

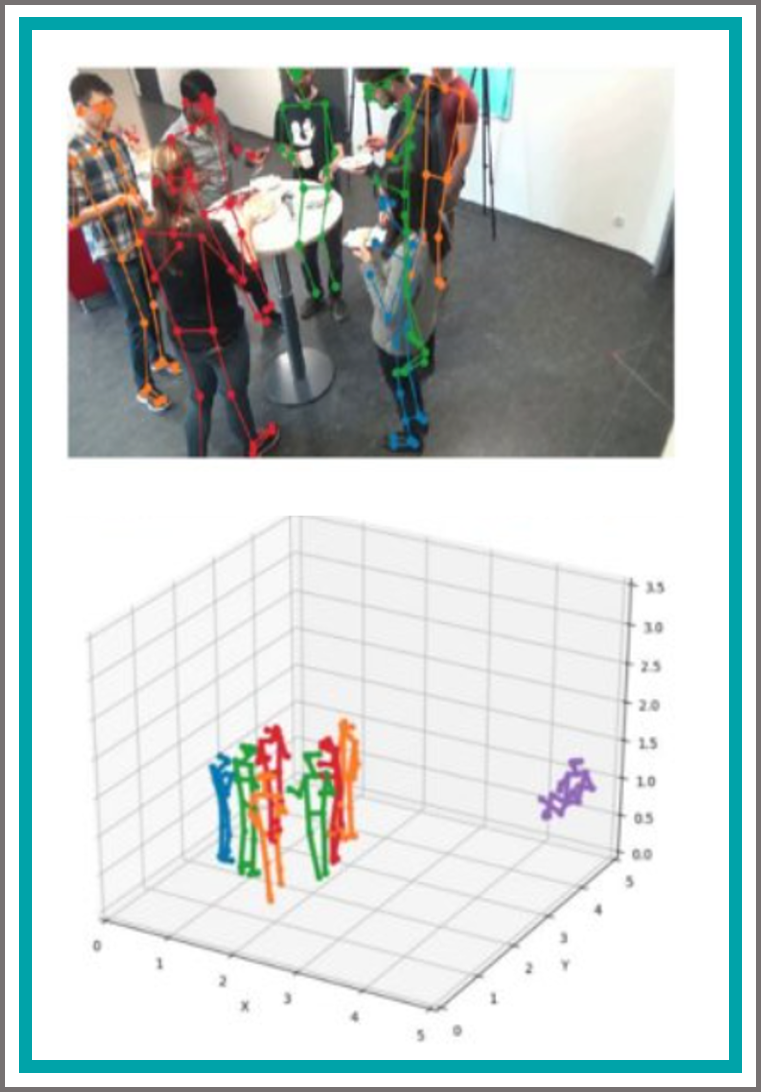
Bonn Activity Maps: Dataset Description
The key prerequisite for accessing the huge potential of current machine learning techniques is the availability of large databases that capture the complex relations of interest. Previous datasets are focused on either 3D scene representations with semantic information, tracking of multiple persons and recognition of their actions, or activity recognition of a single person in captured 3D environments. We present Bonn Activity Maps, a large-scale dataset for human tracking, activity recognition and anticipation of multiple persons. Our dataset comprises four different scenes that have been recorded by time-synchronized cameras each only capturing the scene partially, the reconstructed 3D models with semantic annotations, motion trajectories for individual people including 3D human poses as well as human activity annotations. We utilize the annotations to generate activity likelihoods on the 3D models called activity maps.

Dissertation
Semi-Algebraic Methods for Symbolic Analysis of Complex Reaction Networks
The identification of chemical mechanism that can exhibit oscillatory phenomena in reaction networks are currently of intense interest. In particular, the parametric question of the existence of Hopf bifurcations has gained increasing popularity due to its relation to the oscillatory behavior around the fixed points. However, the detection of oscillations in high-dimensional systems and systems with constraints by the available symbolic methods has proven to be difficult. The development of new efficient methods are therefore required to tackle the complexity caused by the high-dimensionality and non-linearity of these systems. In this thesis, we mainly present efficient algorithmic methods to detect Hopf bifurcation fixed points in (bio)-chemical reaction networks with symbolic rate constants, thereby yielding information about their oscillatory behavior of the networks. The methods use the representations of the systems on convex coordinates that arise from stoichiometric network analysis.
Journal of Computational Physics - Open Access
Detection of Hopf bifurcations in chemical reaction networks using convex coordinates
We present efficient algorithmic methods to detect Hopf bifurcation fixed points in chemical reaction networks with symbolic rate constants, thereby yielding information about the oscillatory behavior of the networks. Our methods use the representations of the systems on convex coordinates that arise from stoichiometric network analysis. One of our methods then reduces the problem of determining the existence of Hopf bifurcation fixed points to a first-order formula over the ordered field of the reals that can be solved using computational logic packages. The second method uses ideas from tropical geometry to formulate a more efficient method that is incomplete in theory but worked very well for the examples that we have attempted; we have shown it to be able to handle systems involving more than 20 species.
Reaction Kinetics, Mechanisms and Catalysis
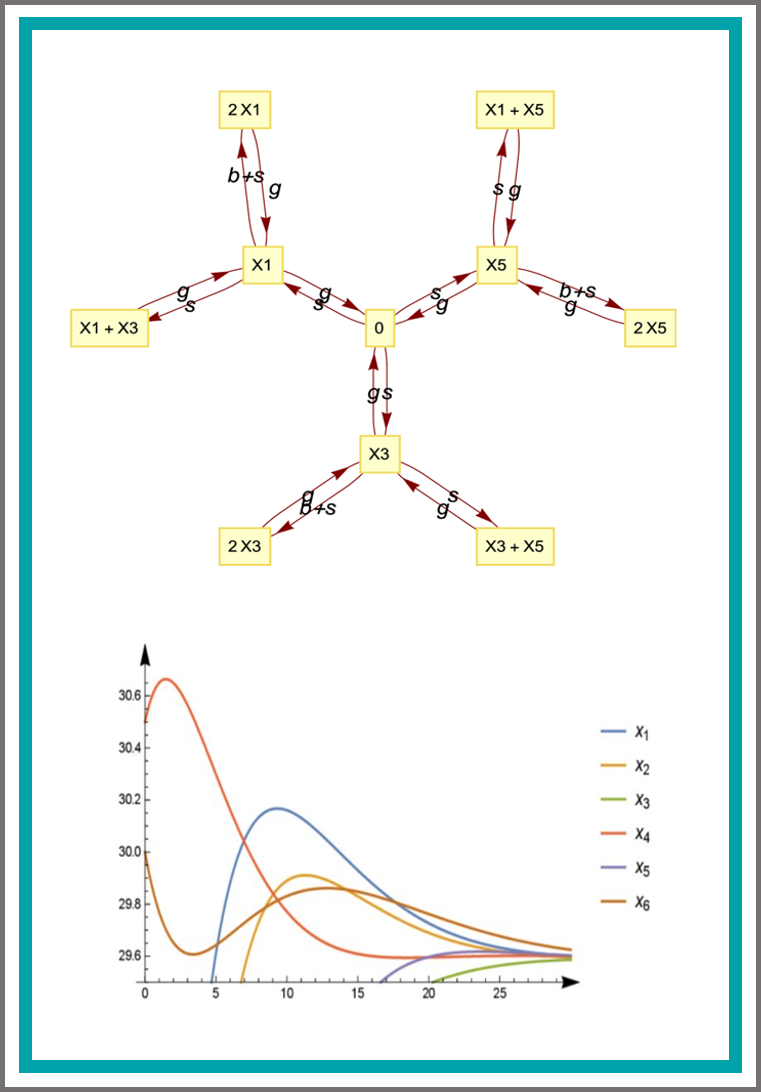
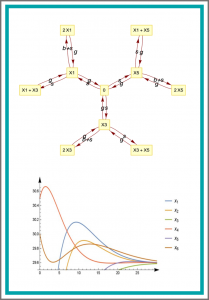
On three genetic repressilator topologies
Novel mathematical models of three different repressilator topologies are introduced. As designable transcription factors have been shown to bind to DNA non-cooperatively, we have chosen models containing non-cooperative elements. The extended topologies involve three additional transcription regulatory elements—which can be easily implemented by synthetic biology—forming positive feedback loops. This increases the number of variables to six, and extends the complexity of the equations in the model. To perform our analysis we had to use combinations of modern symbolic algorithms of computer algebra systems Mathematica and Singular. The study shows that all the three models have simple dynamics that can also be called regular behaviour: they have a single asymptotically stable steady state with small amplitude damping oscillations in the 3D case and no oscillation in one of the 6D cases and damping oscillation in the second 6D case. Using the program QeHopf we were able to exclude the presence of Hopf bifurcation in the 3D system.
Computer Algebra in Scientific Computing - Open Access
Symbolic Versus Numerical Computation and Visualization of Parameter Regions for Multistationarity of Biological Networks
We investigate models of the mitogenactivated protein kinases (MAPK) network, with the aim of determining where in parameter space there exist multiple positive steady states. We build on recent progress which combines various symbolic computation methods for mixed systems of equalities and inequalities. We demonstrate that those techniques benefit tremendously from a newly implemented graph theoretical symbolic preprocessing method. We compare computation times and quality of results of numerical continuation methods with our symbolic approach before and after the application of our preprocessing.

ISSAC
A Case Study on the Parametric Occurrence of Multiple Steady
We consider the problem of determining multiple steady states for positive real values in models of biological networks. Investigating the potential for these in models of the mitogen-activated protein kinases (MAPK) network has consumed considerable effort using special insights into the structure of corresponding models. Here we apply combinations of symbolic computation methods for mixed equality/inequality systems, specifically virtual substitution, lazy real triangularization and cylindrical algebraic decomposition. We determine multistationarity of an 11-dimensional MAPK network when numeric values are known for all but potentially one parameter. More precisely, our considered model has 11 equations in 11 variables and 19 parameters, 3 of which are of interest for symbolic treatment, and furthermore positivity conditions on all variables and parameters.
Computer Algebra in Scientific Computing
Computing Hopf Bifurcations in Chemical Reaction Networks Using Reaction Coordinates
The analysis of dynamic of chemical reaction networks by computing Hopf bifurcation is a method to understand the qualitative behavior of the network due to its relation to the existence of oscillations. For low dimensional reaction systems without additional constraints Hopf bifurcation can be computed by reducing the question of its occurrence to quantifier elimination problems on real closed fields. However deciding its occurrence in high dimensional system has proven to be difficult in practice. In this paper we present a fully algorithmic technique to compute Hopf bifurcation fixed point for reaction systems with linear conservation laws using reaction coordinates instead of concentration coordinates, a technique that extends the range of networks, which can be analyzed in practice, considerably.

Computer Algebra in Scientific Computing
PoCaB: A Software Infrastructure to Explore Algebraic Methods for Bio-chemical Reaction Networks
Given a bio-chemical reaction network, we discuss the different algebraic entities e.g. stoichiometric matrix, polynomial system, deficiency and flux cones which are prerequisite for the application of various algebraic methods to qualitatively analyse them. We compute these entities on the examples obtained from two publicly available bio-databases called Biomodels and KEGG. The computations involve the use of computer algebra tools (e.g. polco, polymake). The results consisting of mostly matrices are arranged in form of a derived database called PoCaB (Platform of Chemical and Biological data). We also present a visualization program to visualize the extreme currents of the flux cone. We hope this will aid in the development of methods relevant for computational systems biology involving computer algebra. The database is publicly available

Algorithmic Aspects of Muldowney's Extension of the Bendixson-Dulac Criterion for Polynomial Vector Fields
n the study of ordinary differential equations the analysis of periodic trajectoriesis seen as an important goal in addition to describing the dynamics around fixedpoints. However, already for two dimensional polynomial systems this questionis related to Hilbert’s 16th problem, which is still unsolved.For the two dimensional case the Bendixson-Dulac criterion gives a sufficientcondition for the non-existence of periodic orbits. This criterion is parameterizedby a Dulac function, and various techniques have been proposed to constructDulac functions, which range form algebraic constructions for special systems totechniques involving the solution of certain partial differential equations.For the higher-dimensional case there are extensions of the criterion ofBendixson-Dulac that also allow the use of Dulac functions. However, lit-tle work seems to have been done to construct Dulac functions in the higherdimensional cases, which was addressed as an important and challenging prob-lem in and stated explicitely as a problem].In the following we will do some first investigations by systematical evalu-ations of possible low-degree polynomial and rational functions as Dulac testfunctions. We will restrict ourselves to examples arising in the life sciences, inwhich the positive real cone is an invariant subspace and is the area of interest.

Computer Algebra in Scientific Computing
On Muldowney's Criteria for Polynomial Vector Fields with Constraints
We study Muldowney’s extension of the classical Bendixson-Dulac criterion for excluding periodic orbits to higher dimensions for polynomial vector fields. Using the formulation of Muldowney’s sufficient criteria for excluding periodic orbits of the parameterized vector field on a convex set as a quantifier elimination problem over the ordered field of the reals we provide case studies of some systems arising in the life sciences. We discuss the use of simple conservation constraints and the use of parametric constraints for describing simple convex polytopes on which periodic orbits can be excluded by Muldowney’s criteria.